ЛЕКЦИЯ 25

Массу тела можно определить путем измерения испытываемого телом ускорения a под действием известной силы F

Определяемая таким путем масса M_ин известна под названием инертной массы.

Массу можно также определить, измеряя силу ее тяготения к другому телу, например, к Земле

Определяемая таким образом масса M_гр носит название гравитационой массы. В формуле (2) M_З — масса Земли, а R_З — её радиус.

Замечательно, что инертные массы всех тел в пределах точности измерений пропорциональны их гравитационным массам. ¹ Простейший опыт по проверке сказанного заключается в выяснении того, действительно ли все тела падают с одинаковым ускорением. Для одного тела, падающего вблизи поверхности Земли, имеем

$\frac{M_{ин}(1)\cdot a(1)}{M_{ин}(2)\cdot a(2)} = \frac{M_{гр}(1)}{M_{гр}(2)} ,$

(5)

$\frac{M_{ин}(1)}{M_{гр}(1)} = \frac{M_{ин}(2)}{M_{гр}(2)} \cdot\frac{a(2)}{a(1)} .$

(6)

Но опыт показывает, что в вакууме все тела падают одинаково, так что в пределах точности измерений

т.е. отношение инертной и гравитационной масс одинаково для всех тел. Мы можем всегда привести это отношение к 1 путем выбора подходящего значения для гравитационной константы G.

Одним из первых проверил равенство инертной и гравитационной масс сам Ньютон в своих классических опытах с маятником. Маятники одинаковой длины с грузом одинакового веса на конце имели одинаковые периоды колебаний, что свидетельствовало о равенстве инертной и гравитационной масс. ²

Среди других опытов следует отметить остроумные опыты Этвеша, начатые в 1890 г. и продолжавшиеся около 25 лет. Рассмотрим сначала поведение маятника, подвешенного у поверхности Земли на широте 45^° (см. рис. 1).

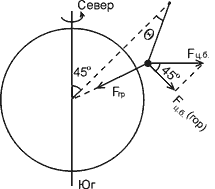Рис. 1. Маятник.

На шарик маятника действует сила гравитационного притяжения, направленного к центру Земли

и центробежная сила, направленная перпендикулярно оси вращения Земли вокруг своей оси

$F_{ц.б.} = M_{ин}\Omega^2R_З\cos45^{\circ}= M_{ин}\Omega^2R_З/\sqrt{2} .$

(10)

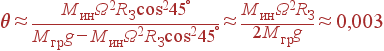$\theta\approx \frac{M_{ин}\Omega^2R_З\cos^245^{\circ}} {M_{гр}g-M_{ин}\Omega^2R_З\cos^245^{\circ}} \approx \frac{M_{ин}\Omega^2R_З}{2M_{гр}g}\approx 0{,}003$

(11)

Предположим теперь, что крутильный подвес состоит из двух шариков, сделанных из различного материала, но одинаковой гравитационной массы M_гр(1) = M_гр(2).

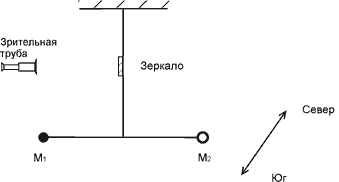Рис. 2. Крутильный подвес.

Если M_ин(1)≠ M_ин(2), то под действием неуравновешенных центробежных сил (горизонтальная компонента) крутильная нить будет закручиваться. Измерение повторяется после поворота прибора на 180^°. Это позволяет определить нулевое положение весов. Данный метод — характерный пример нулевого метода измерений: эффект наблюдается только при M_ин(1)≠ M_ин(2).

Этвеш произвел сравнение восьми разных материалов с платиной, принятой за эталон. Он установил, что

с относительной ошибкой менее 10^–8. Недавние опыты Дике (1961-1964 гг.) подтвердили равенство обоих видов масс с точностью до 10^–10.

Наряду с фундаментальным физическим значением независимость ускорения от массы тела имеет и большое практическое значение. Например, следствием этого является невесомость в космическом корабле. Разница в инертной и гравитационной массах сделала бы невозможной космические полеты. Разные части корабля подвергались бы действию различных ускорений, возникали бы перегрузки, напряжения и т.д.

Принцип эквивалентности

Таким образом, мы приходим к фундаментальному выводу о том, что гравитационные поля или поля тяготения обладают следующим основным свойством:

все тела, вне зависимости от их массы, движутся в них (при заданных начальных условиях) одинаковым образом.

Например, законы свободного падения в поле тяготения Земли одинаковы для всех тел, какой бы массой они не обладали, все они приобретают одно и то же ускорение.

Это свойство гравитационных полей дает возможность установить существенную аналогию между движением тел в гравитационном поле и движением тел, не находящихся в каком-либо внешнем поле, но рассматриваемых с точки зрения неинерциальной системы отсчета. Действительно, в инерциальной системе отсчета свободное движение всех тел происходит прямолинейно и равномерно, и если, скажем, в начальный момент времени их скорости были одинаковыми, то они будут одинаковыми все время. Очевидно, поэтому, что если рассматривать это движение в заданной неинерциальной системе, то и относительно неё все тела будут двигаться одинаковым образом.

Таким образом, свойства движения в неинерциальной системе отсчета такие же, как в инерциальной системе при наличии гравитационного поля. Другими словами,

неинерциальная система отсчета эквивалентна некоторому гравитационному полю.

Это обстоятельство называют принципом эквивалентности.

Рассмотрим, например, движение в равномерно ускоренной системе отсчета. Свободно движущиеся в ней тела любой массы будут, очевидно, обладать относительно этой системы одинаковым постоянным ускорением, равным и противоположным ускорению самой системы отсчета.

Таким же является движение в однородном постоянном гравитационном поле, например, в поле тяготения Земли (в небольших участках его, где поле можно рассматривать как однородное). Таким образом,

равномерно ускоренная система отсчета эквивалентна постоянному однородному внешнему полю.

В таком же смысле неравномерно ускоренная поступательно движущаяся система отсчета эквивалентна однородному, но переменному гравитационному полю.

Однако поля, которым эквивалентны неинерциальные системы отсчета, все же не вполне тождественны с "истинными" гравитационными полями, существующими и в неинерциальных системах. Между ними имеется существенное отличие в отношении их свойств на бесконечности. На бесконечном расстоянии от создающих поле тел "истинное" гравитационное поле всегда стремится к нулю. Поля же, которым эквивалентны неинерциальные системы отсчета, на бесконечности, напротив, неограниченно возрастают или, в крайнем случае, остаются конечными по величине. Так, например, возникающие во вращающейся системе отсчета центробежные силы неограниченно растут при удалении от оси вращения; поле, которому эквивалентна ускоренно прямолинейно движущаяся система отсчета, одинаково во всем пространстве, в том числе и на бесконечности.

Поля, которым эквивалентны неинерциальные системы отсчета, исчезают, как только мы перейдем к инерциальной системе. В противоположность этому, "истинные" гравитационные поля (существующие и в инерциальной системе отсчета) невозможно исключить никаким выбором системы отсчета. Это видно уже из указанного выше различия между условиями на бесконечности в "истинных" гравитационных полях и в полях, которым эквивалентны неинерциальные системы; поскольку последние на бесконечности к нулю не стремятся, то ясно, что

никаким выбором системы отсчета нельзя исключить "истинные" поля, обращающиеся на бесконечности в нуль.

Единственное, чего можно достичь надлежащим выбором системы отсчета, это

исключения гравитационного поля в данном участке пространства, достаточно малом для того, чтобы в нем можно было считать поле однородным.

Это можно сделать путем выбора ускоренно движущейся системы, ускорение которой было бы равно тому ускорению, которое приобретает частица, помещенная в рассматриваемом участке поля.

Таким образом, для наблюдателя в свободно падающем лифте все законы физики такие же, как и в инерциальных системах отсчета специальной теории относительности (по крайней мере, в непосредственном соседстве с центром лифта, т.е. локально).

Действие ускоренного движения и силы тяжести полностью взаимно уничтожаются. Наблюдатель, сидящий в закрытом лифте и регистрирующий силы, представляющиеся ему гравитационными, не может сказать, какая доля этих сил обусловлена ускорением и какая — действительными гравитационными силами. Он вообще не обнаружит никаких сил, если только на лифт не подействуют какие-либо другие (т.е. отличные от гравитационных) силы.

Искривление луча света в гравитационном поле

Из принципа эквивалентности следуют два важных вывода о распространении света в гравитационном поле.

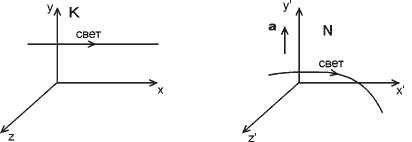Рассмотрим сначала первый эффект. Пусть в некоторой инерциальной системе K параллельно оси x распространяется луч света.

Рис. 3. Искривление луча света в неинерциальной системе отсчета.

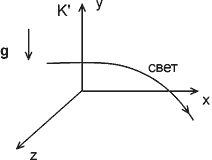Рассмотрим тот же процесс в неинерциальной системе отсчета N, движущейся с ускорением a вверх вдоль оси y. Ясно, что в этой системе отсчета траектория луча света не является прямой. Луч отклоняется в направлении, противоположном направлению ускорения системы отсчета N. Но, согласно принципу эквивалентности, равномерно ускоренная система отсчета N эквивалентна однородному гравитационному полю, вызывающему ускорение g = –a. То есть, если бы в инерциальной системе K было бы еще однородное гравитационное поле (система K'), то свет при своем распространении отклонялся бы от прямой линии в направлении ускорения g.

Рис. 4. Отклонение луча света в однородном гравитационном поле.

Таким образом, все выглядело бы так, как если бы фотоны обладали бы гравитационной массой. Оказывается, что так оно и есть. Согласно формуле Эйнштейна ${\cal E}=m_{ин}c^2$ , т.е. если есть энергия ${\cal E}$ , то с ней связана инертная масса

Но энергия фотона равна, как известно, величине ħω, где ω — частота фотона. Следовательно, инертная масса фотона равна

Согласно принципу эквивалентности она должна быть равна гравитационной массе фотона

Таким образом, за счет наличия у фотона гравитационной массы свет отклоняется гравитационным полем. Заметить это отклонение можно, например, наблюдая прохождение луча света около Солнца. В этом случае эффект будет максимальным.

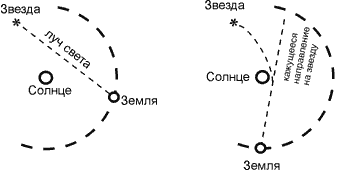Рис. 5. Отклонение света в гравитационном поле Солнца.

Оценить величину эффекта отклонения можно с помощью классической механики, приписав фотону массу m_ф.

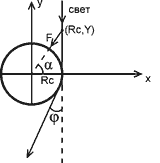Рис. 6. Классический расчет эффекта отклонения.

Предположим, что свет проходит мимо Солнца с прицельным расстоянием R_c (отсчитанным от центра Солнца). Поперечная гравитационная сила, действующая на фотон в положении (R_c, y) равна

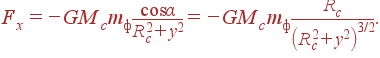$F_x=-GM_cm_ф\frac{\cos\alpha}{R_c^2+y^2}= -GM_cm_ф\frac{R_c}{\left(R_c^2+y^2 \right)^{3/2}} .$

(16)

Конечное значение поперечной составляющей скорости фотона определяется через поперечную составляющую приращения импульса вдоль оси x

$\begin{array}{lcl} &&m_фv_x = \displaystyle \int F_xdt = \int F_x\frac{dy}{dy/dt} = \int F_x\frac{dy}{v_y} = \int F_x\frac{dy}{c} =\\[20pt] && -\displaystyle\frac{GM_cm_ф}{c}R_c \int\limits_{-\infty}^{+\infty} \frac{dy}{\left(y^2+R_c^2 \right)^{3/2}} = -\frac{2GM_cm_ф}{R_cc} \underbrace{\int\limits_0^{\infty}\frac{d\xi} {\left(\xi^2+1 \right)^{3/2}}}_{=1} \end{array}$

(17)

(последний определенный интеграл равен 1, поскольку первообразная подинтегральной функции равна $\xi/\sqrt{1+\xi^2}$ ). Отсюда находим угол отклонения

$\varphi=\frac{|v_x|}{c}\simeq \frac{2GM_c}{R_cc^2}\approx 0{,}87^{ \prime\prime} .$

(18)

Более точные вычисления, основанные на специальной теории относительности и принципе эквивалентности, предсказывают в два раза большее значение: 1,75^''. Этот результат был экспериментально проверен для света (наблюдения велись во время солнечных затмений) и подтвердился с точностью около 20%. Позднее для радиоволн была достигнута бóльшая точность, порядка 5%–10%.

Изменение частоты света при движении в гравитационном поле

Второй эффект — изменение частоты света в гравитационном поле — заключается в следующем. Пусть наблюдатель, находящийся на Земле, посылает световой сигнал наблюдателю, находящемуся на некоторой высоте над поверхностью Земли, например, на вершине высокой башни (см. рис. 7).

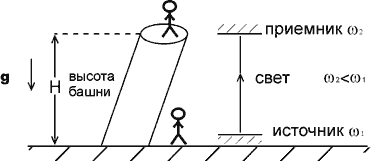Рис. 7. Изменение частоты света в гравитационном поле.

Эффект состоит в том, что наблюдатель на башне измерит несколько меньшую частоту, чем та, которая была послана наблюдателем с Земли. Это есть так называемое гравитационное красное смещение.

Объяснение этого эффекта заключается в следующем. Гравитационное поле g эквивалентно неинерциальной системе отсчета, движущейся вверх с ускорением a = –g. Пусть расстояние между наблюдателями (находящимися в ракете, движущейся с ускорением a) равно H. Для определенности предположим, что, когда нижний наблюдатель послал фотон, ракета покоилась в некоторой инерциальной системе координат. Чтобы достигнуть верхнего наблюдателя, фотону требуется время

За это время верхний наблюдатель приобретет скорость

Поэтому, в силу эффекта Доплера, он зарегистрирует фотон с меньшей частотой ω₂:

$\frac{\Delta\omega}{\omega}\equiv \frac{\omega_1 - \omega_2}{\omega_1} = \frac{v}{c}=\frac{gH}{c^2} .$

(22)

К такому же результату приводят рассуждения, использующие инертную массу фотона, которая равна гравитационной. При распространении фотона вверх его энергия m_ф1c² = (ħω₁/c²)c² уменьшается на величину m_ф1gH и становится равной

$m_{ф2}c^2=\frac{\hbar\omega_2}{c^2}c^2= \frac{\hbar\omega_1}{c^2}c^2-m_{ф1}gH ,$

(23)

$\omega_2=\omega_1-\frac{\omega_1}{c^2}gH = \omega_1\left(1-\frac{gH}{c^2} \right) ,$

(24)

Интересно, что Эйнштейн пришел к этому результату, исходя из закона сохранения энергии. Пусть частица из точки A свободно падает в точку B, находящуюся под ней на расстоянии H.

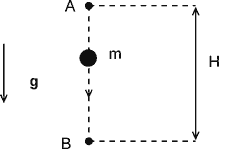Рис. 8. "Свободное падение" частицы с высоты H.

Пусть теперь в точке B частица аннигилирует, превращаясь в фотон с той же энергией

и летит снова вверх. Если фотон никак не взаимодействует с полем тяготения, то его энергия в точке A будет такая же, что и в точке B. В точке A с помощью соответствующей аппаратуры он может быть превращен в другую частицу с такой же энергией и весь процесс повторится сначала. Таким образом, энергия частицы будет все нарастать и нарастать. Если научиться её отнимать, то получим вечный двигатель. Выход из этого противоречия как раз и заключается в предположении, что при распространении в гравитационном поле (против силы тяжести) свет испытывает красное смещение в соответствии с полученными формулами.

Эффект красного смещения очень мал. Так если H = 20 м, то относительное изменение частоты

$\frac{\Delta\omega}{\omega}=\frac{gH}{c^2}\approx \frac{10^3\cdot 2\cdot 10^3}{(3\cdot 10^{10})^2}\approx 2\cdot 10^{-15} .$

(28)

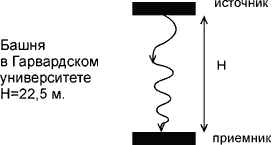Однако этот фантастически малый эффект был действительно измерен Паундом и Ребкой в 1960 г. для гамма-лучей (используя эффект Мëссбауэра). Башня в Гарвардском университете имела высоту 22,5 м, и частота используемых гамма-квантов ω_γ = 2,2· 10¹⁹ сек^–1 .

Рис. 9. Опыт Паунда и Ребки.

Отношение измеренного изменения частоты к предсказанному теорией значению (28) было равно

$\frac{(\Delta\nu)_{эксп}}{(\Delta\nu)_{теор}} = 1{,}05\pm 0{,}10 .$

(29)

Следствием гравитационного красного смещения является то, что фотон частоты ω, покидающий звезду и уходящий в бесконечность, будет восприниматься в бесконечности с частотой

где M_зв — масса звезды, а R_зв — радиус звезды.

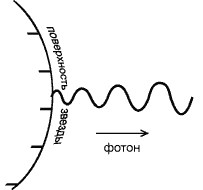Рис. 10. Улетая в бесконечность с поверхности звезды, фотон теряет энергию. Его частота при этом уменьшается.

У белых карликов значение отношения M_зв/R_зв велики, вследствие чего они отличаются сравнительно большими величинами красного смещения. Так для Сириуса B вычисленное относительное смещение составляет

а измеренное равно –6,6· 10^–5. Расхождение не выходит за пределы возможной ошибки в определении величин M_зв и R_зв.

¹ Путем соответствующего подбора величины G можно добится того, чтобы инертные массы были равны гравитационным.

² Покажите, что частота малых колебаний маятника 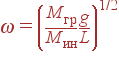$\omega=\left(\frac{M_{гр}}{M_{ин}} \frac gL\right)^{1/2}$ . Если бы при одинаковом весе, т.е. одинаковых M_гр, инертные массы двух любых тел не совпадали бы, то это приводило бы к различию в их периодах колебаний.

ЛЕКЦИЯ 25

Равенство инертной и гравитационной масс

Принцип эквивалентности

Искривление луча света в гравитационном поле

Изменение частоты света при движении в гравитационном поле